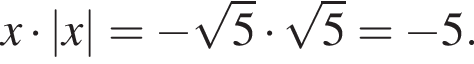Укажите номер рисунка, на котором изображен равнобедренный треугольник.
Образующая конуса равна 26 и наклонена к плоскости основания под углом 60°. Найдите площадь боковой поверхности конуса.
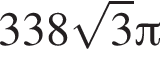

Выразите a из равенства 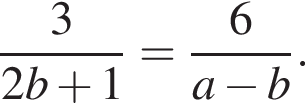
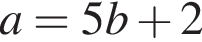
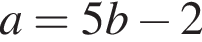
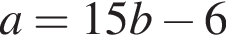
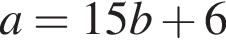

Даны пары значений переменных x и y: (3; 9); (−15; 3); (0; 12); (14; −2); (6; 6). Укажите пару, которая НЕ является решением уравнения x + y = 12.
Определите координату точки А, изображенной на координатной прямой.
Свежие фрукты при сушке теряют a % своей массы. Укажите выражение, определяющее массу сухих фруктов (в килограммах), полученных из 20 кг свежих.
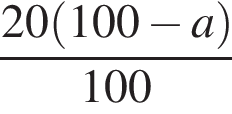
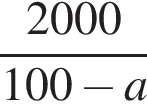
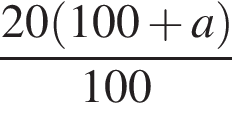
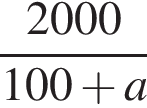
На одной стороне прямого угла О отмечены две точки А и В так, что ОА = 1,7, OB = а, ОА < ОВ. Составьте формулу, по которой можно вычислить радиус r окружности, проходящей через точки А, В и касающейся другой стороны угла.
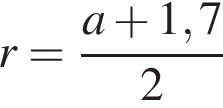
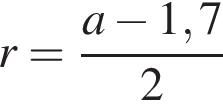
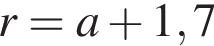
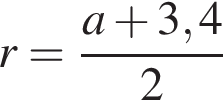
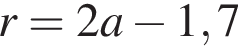
Последовательность (an) задана формулой n-ого члена an = 3n−1 · (7 − n). Найдите пятый член этой последовательности.
Упростите выражение  если
если ![]() и
и ![]()

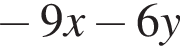
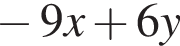

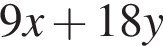
Найдите наибольшее натуральное двузначное число, которое при делении на 11 дает в остатке 7.
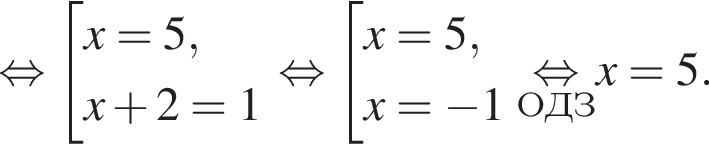
Решите уравнение  В ответ запишите сумму его корней (корень, если он один).
В ответ запишите сумму его корней (корень, если он один).
Выберите все верные утверждения, являющиеся свойствами нечетной функции ![]() определённой на
определённой на  и заданной формулой
и заданной формулой 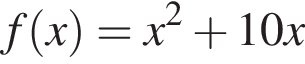 при
при ![]()
1. Функция имеет три нуля.
2. Функция убывает на промежутке [6; 9].
3. Максимум функции равен 25.
4. Минимальное значение функции равно -25.
5. 
6. Функция принимает отрицательные значения при 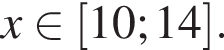
7. График функции симметричен относительно оси абсцисс.
Ответ запишите в виде последовательности цифр в порядке возрастания. Например: 123.
Для начала каждого из предложений подберите его окончание 1-5 так, чтобы получилось верное утверждение.
A) Значение выражения 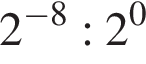 равно:
равно:
Б) Значение выражения 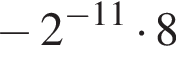 равно:
равно:
В) Значение выражения 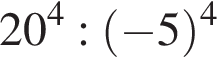 равно:
равно:
1) 256
2) −256
3) ![]()
4) ![]()
5) 32
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
На круговой диаграмме представлена информация о продаже 200 кг овощей в течение дня. Для начала каждого из предложений А — В подберите его окончание 1 — 6 так, чтобы получилось верное утверждение.
А) Масса (в килограммах) проданной капусты равна ...
Б) Отношение, выраженное в процентах, которое показывает, на сколько масса проданного картофеля меньше массы проданных помидоров, равно ...
В) Отношение, выраженное в процентах, которое показывает, на сколько масса проданной свеклы больше массы проданного лука, равно ...
1) 25
2) 40
3) 4
4) 125
5) 38
6) 19
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
Градусная мера угла ABC равна 126°. Внутри угла ABC проведен луч BD, который делит данный угол в отношении 1 : 6 (см. рис.). Найдите градусную меру угла 1, если BO — биссектриса угла DBC.
В основании прямой четырехугольной призмы ABCDA1B1C1D1 лежит трапеция ABCD, у которой ∠C = 90°, BC и AD — основания, BC = CC1. Плоскость, которая проходит через ребро DC и вершину A1 призмы, образует угол
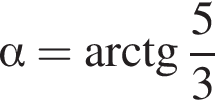 с плоскостью основания (см. рис.) и отсекает часть NC1CA1D1D. Если объем призмы равен 48, то объем оставшейся части равен … .
с плоскостью основания (см. рис.) и отсекает часть NC1CA1D1D. Если объем призмы равен 48, то объем оставшейся части равен … .
По двум перпендикулярным прямым, которые пересекаются в точке O, движутся две точки M1 и M2 по направлению к точке O со скоростями 1 ![]() и 2
и 2 ![]() соответственно. Достигнув точки O, они продолжают свое движение. В первоначальный момент времени M1O = 5 м, M2O = 20 м. Через сколько секунд расстояние между точками M1 и M2 будет минимальным?
соответственно. Достигнув точки O, они продолжают свое движение. В первоначальный момент времени M1O = 5 м, M2O = 20 м. Через сколько секунд расстояние между точками M1 и M2 будет минимальным?
Найдите периметр правильного шестиугольника, меньшая диагональ которого равна ![]()
Найдите значение выражения 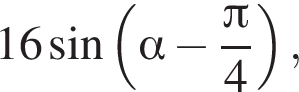 если
если 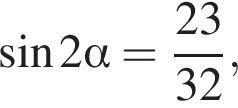
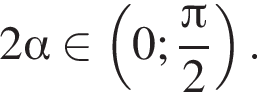
Пусть (x1; y1), (x2; y2) — решения системы уравнений 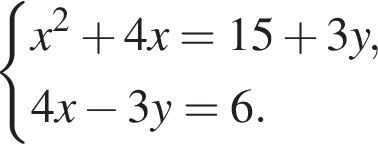
Найдите значение выражения 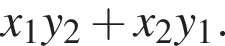
Найдите сумму корней уравнения 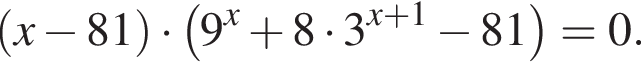
Найдите произведение наибольшего решения на количество решений уравнения 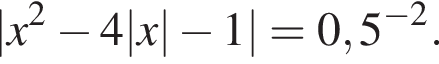
Найдите значение выражения 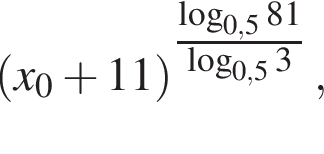 где x0 — корень уравнения
где x0 — корень уравнения 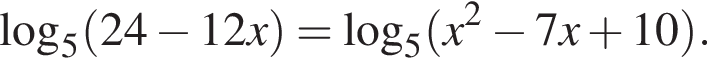
На рисунке изображен график функции 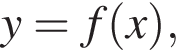 заданной на промежутке
заданной на промежутке 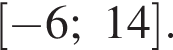 Найдите произведение значений аргумента, при которых
Найдите произведение значений аргумента, при которых 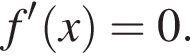 (Черными точками отмечены узлы сетки, через которые проходит график функции
(Черными точками отмечены узлы сетки, через которые проходит график функции 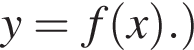
Длины сторон параллелограмма относятся как 2 : 3, а высота, проведенная к большей стороне, равна 6. Найдите значение выражения ![]() где S — площадь параллелограмма, если один из углов параллелограмма равен 120°.
где S — площадь параллелограмма, если один из углов параллелограмма равен 120°.
Пусть 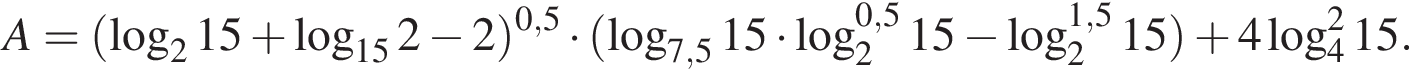
Найдите значение выражения 2A.
Прямая, проходящая через вершину К треугольника KMN, делит его медиану MA в отношении 8 : 3, считая от вершины M, и пересекает сторону MN в точке B. Найдите площадь треугольника KMN, если площадь треугольника KMB равна 16.
Найдите (в градусах) наименьший корень уравнения 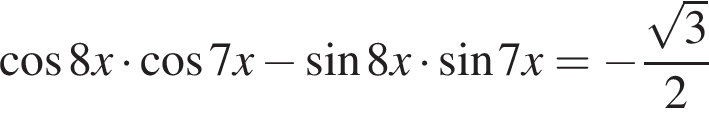 на промежутке
на промежутке 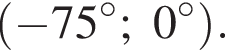
При делении некоторого натурального двузначного числа на сумму его цифр неполное частное равно 6, а остаток равен 7. Если цифры данного числа поменять местами и полученное число разделить на сумму его цифр, то неполное частное будет равно 4, а остаток будет равен 6. Найдите исходное число.
Решите уравнение
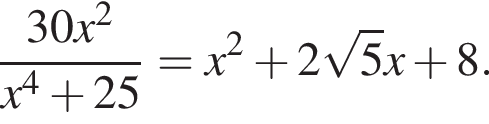
В ответ запишите значение выражения ![]() где x — корень уравнения.
где x — корень уравнения.

 — все углы разные.
— все углы разные. — все углы разные.
— все углы разные. — треугольник равнобедренный.
— треугольник равнобедренный. — все углы разные.
— все углы разные. — все углы разные.
— все углы разные. где r — радиус основания, l — образующая. Найдем радиус:
где r — радиус основания, l — образующая. Найдем радиус:  Таким образом, площадь боковой поверхности равна:
Таким образом, площадь боковой поверхности равна: 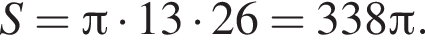
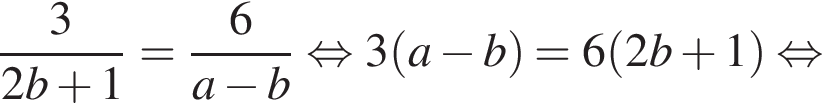
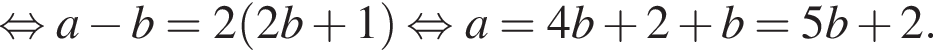
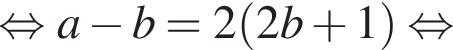
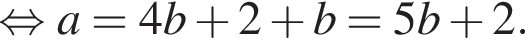
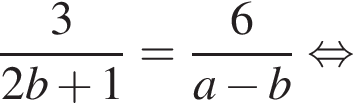

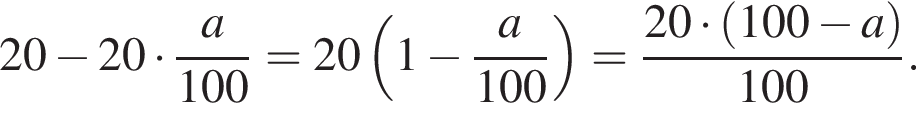
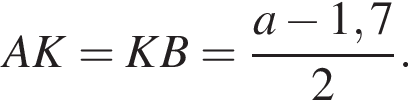
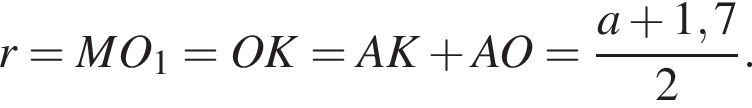
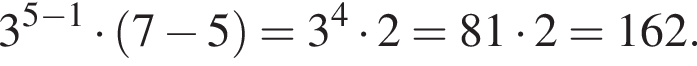
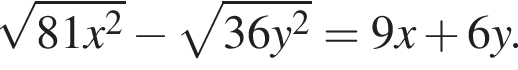
 Так как нужно найти наибольшее натуральное двузначное число, то a < 100. Решим неравенство:
Так как нужно найти наибольшее натуральное двузначное число, то a < 100. Решим неравенство: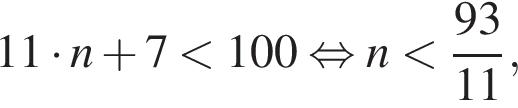
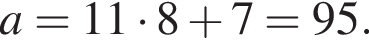
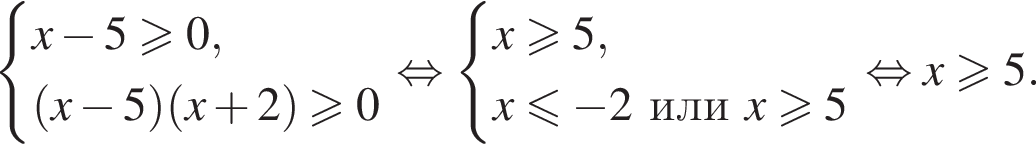
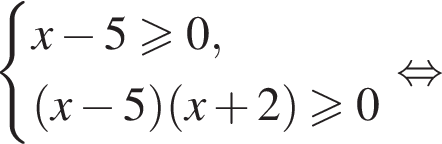
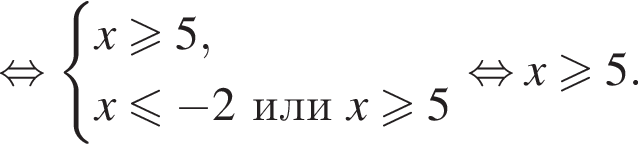
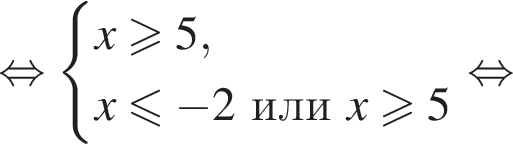
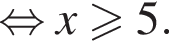
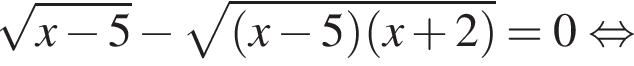
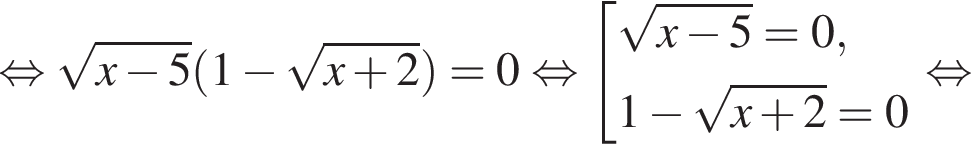

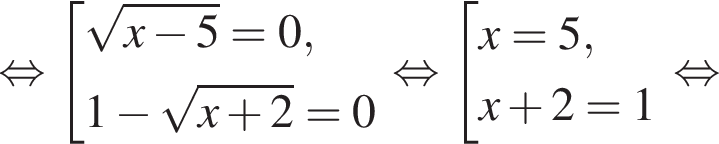
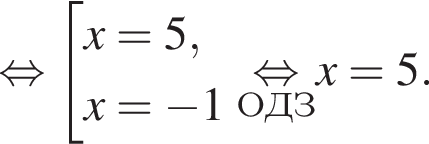
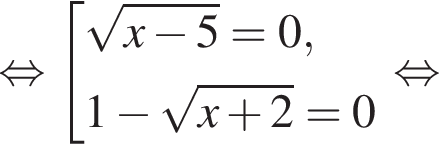
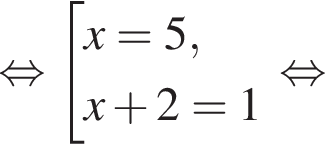
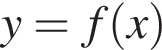 при
при 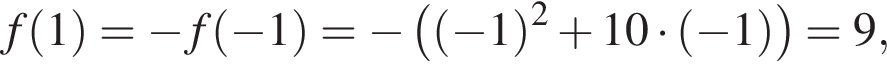
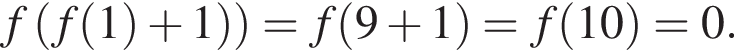 Утверждение 5 верно.
Утверждение 5 верно.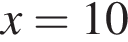 функция равна нулю, а значит, принимает отрицательные значения не во всех точках отрезка
функция равна нулю, а значит, принимает отрицательные значения не во всех точках отрезка 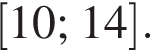 Утверждение 6 неверно.
Утверждение 6 неверно.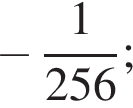
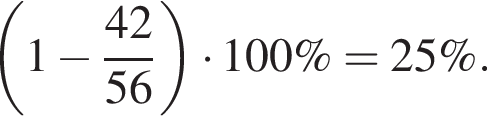
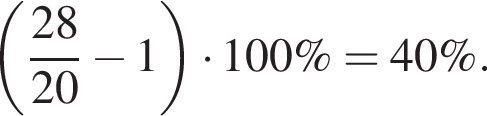
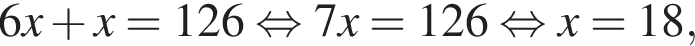
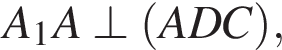
 следовательно, по теореме о трех перпендикулярах
следовательно, по теореме о трех перпендикулярах 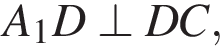 поэтому
поэтому  откуда
откуда 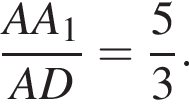 Пусть
Пусть 
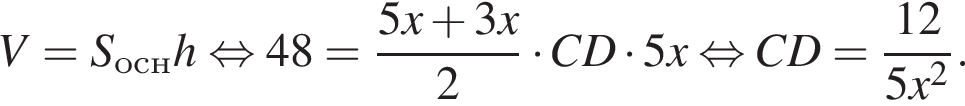
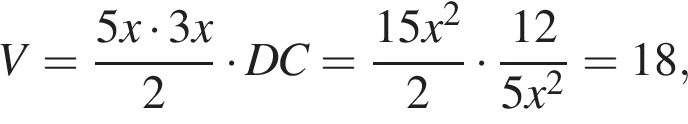 откуда
откуда 
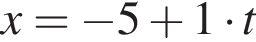 (м) и
(м) и 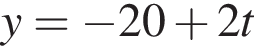 (м).
(м).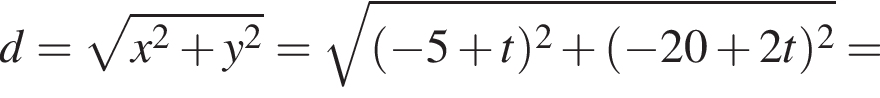
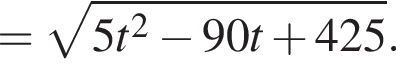
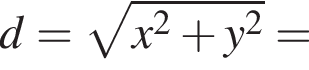
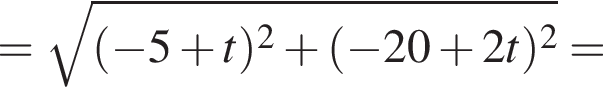
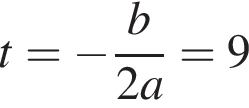 и в этой точке положительно:
и в этой точке положительно: 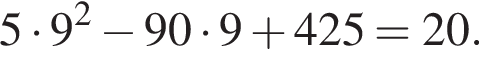 Таким образом, при
Таким образом, при 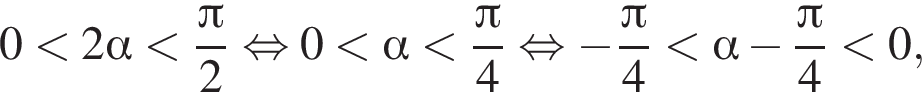

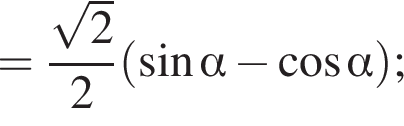
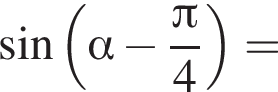
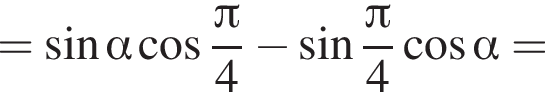
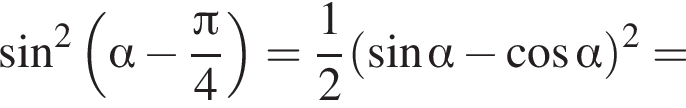
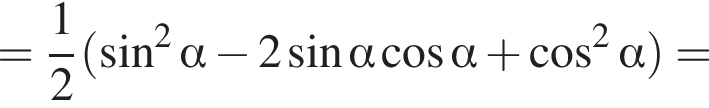
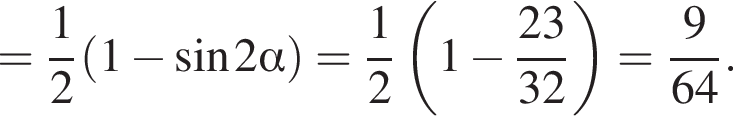
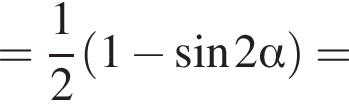
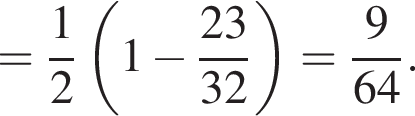
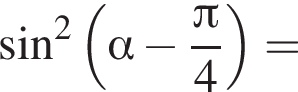
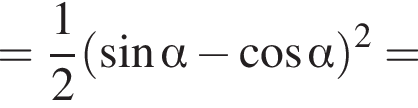
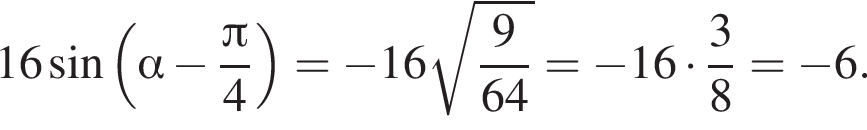
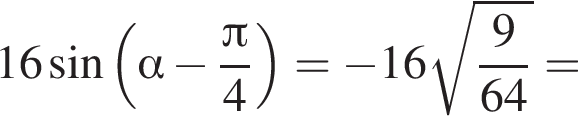
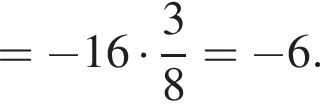
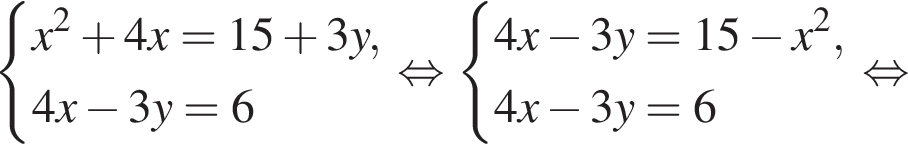
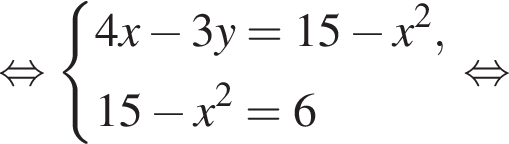
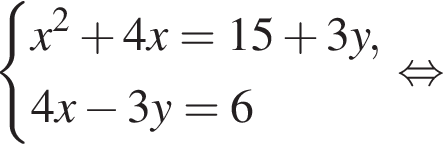
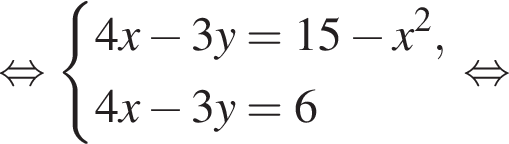
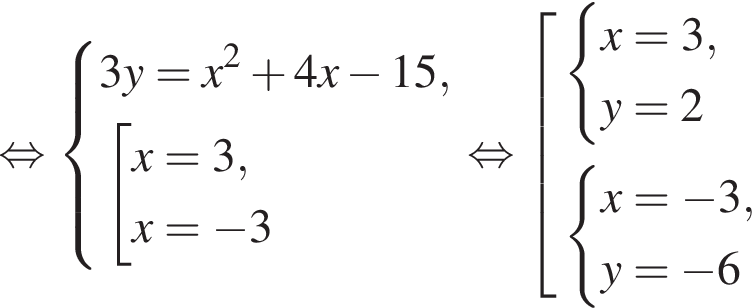

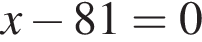 следует, что первый корень
следует, что первый корень  Рассмотрим
Рассмотрим 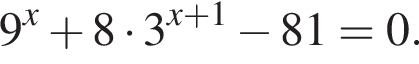 Сделаем замену
Сделаем замену  Тогда:
Тогда:
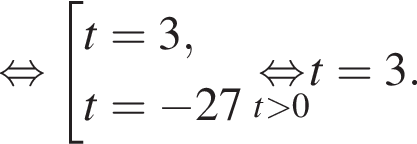

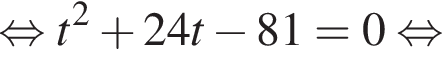
 Отсюда следует, что сумма корней уравнения равна 82.
Отсюда следует, что сумма корней уравнения равна 82.
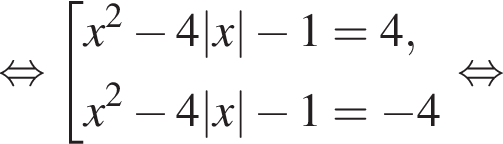
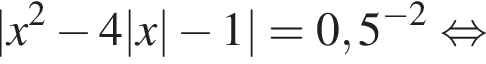
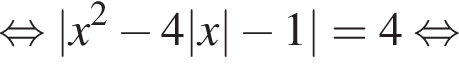
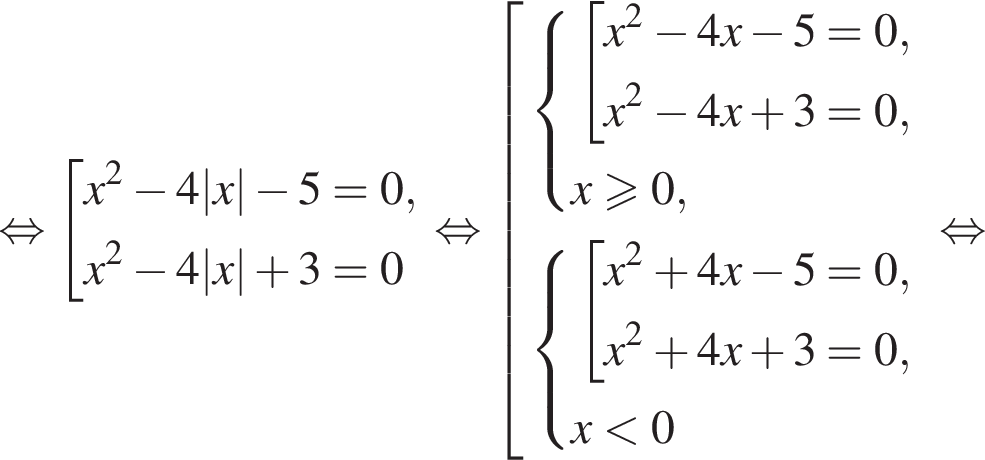
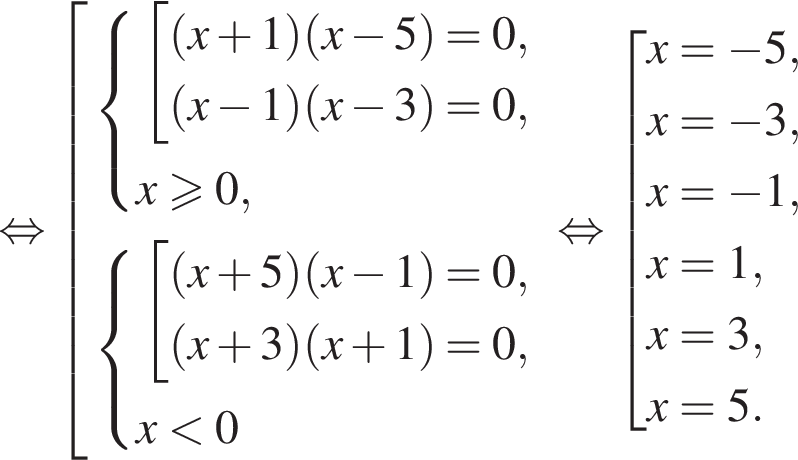
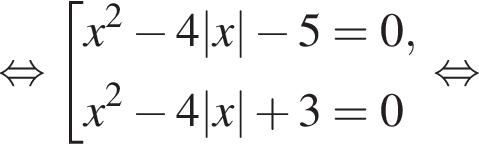
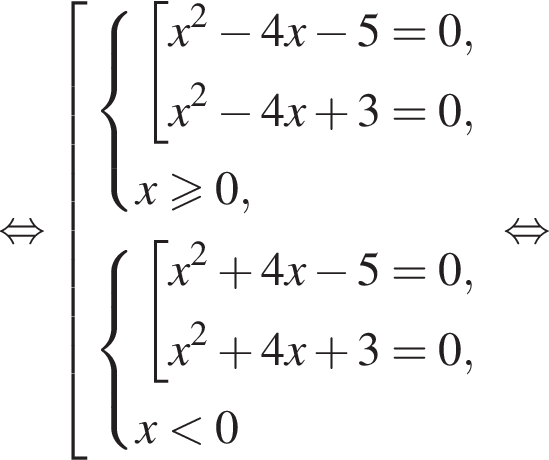
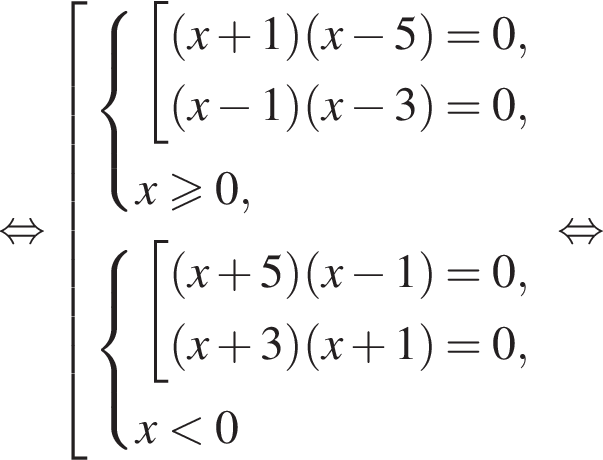
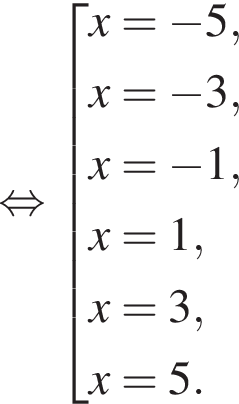
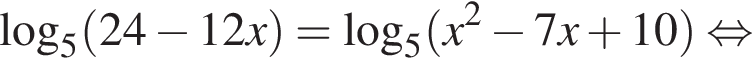
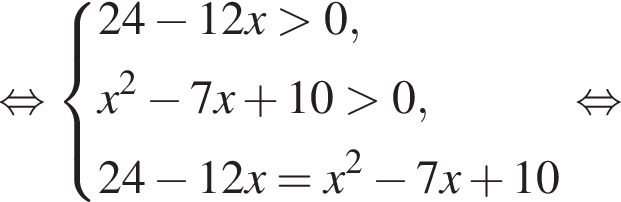
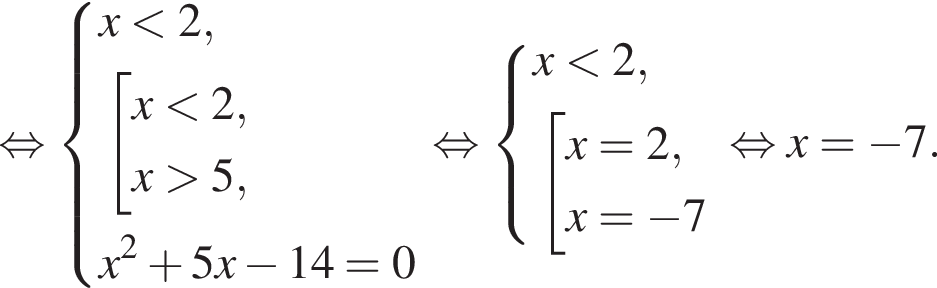
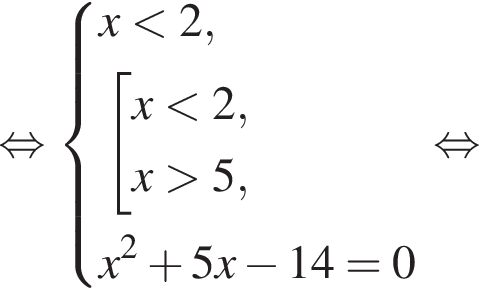
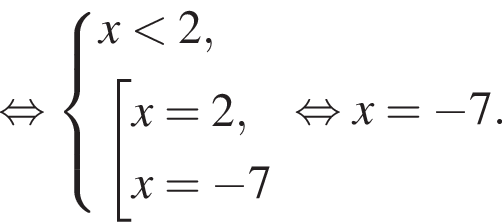
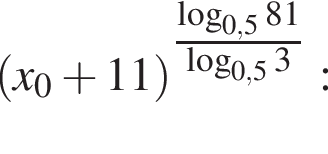
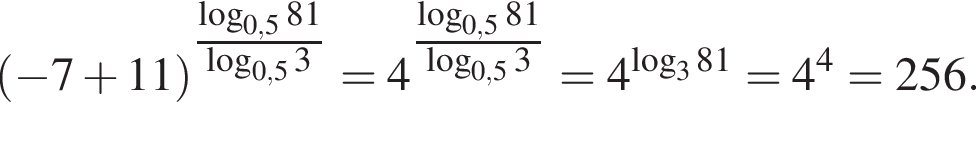
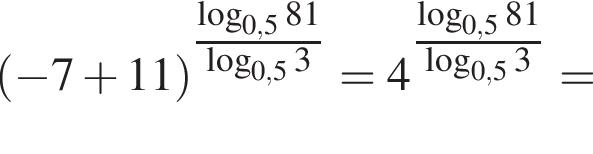


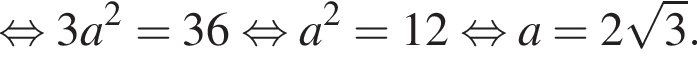
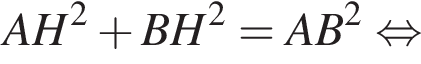
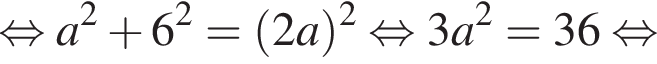
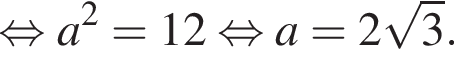
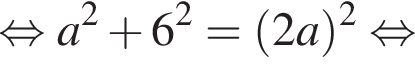
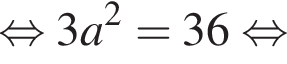
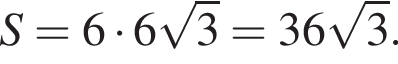 Значение выражения
Значение выражения 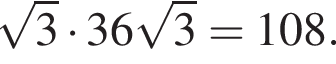

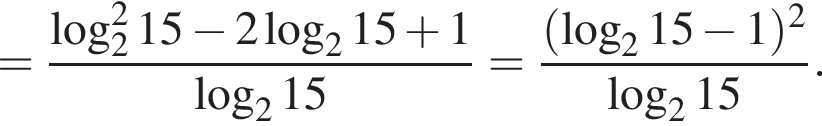
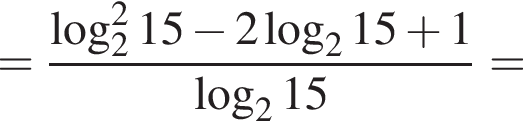
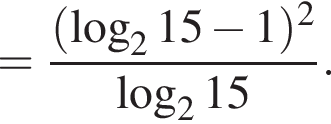
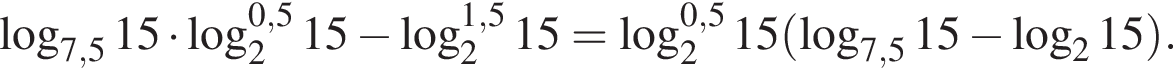
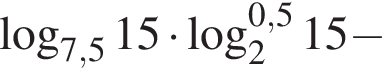
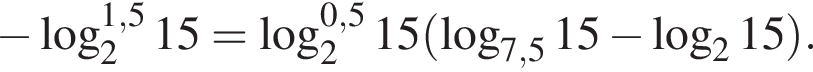
 Тогда имеем:
Тогда имеем: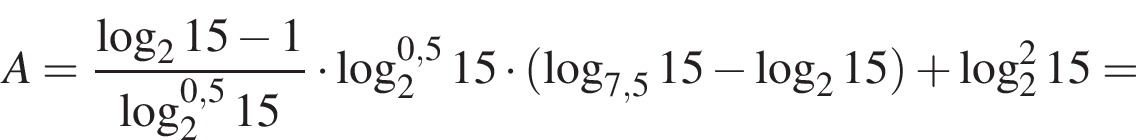
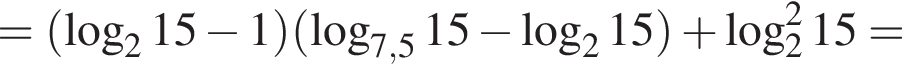
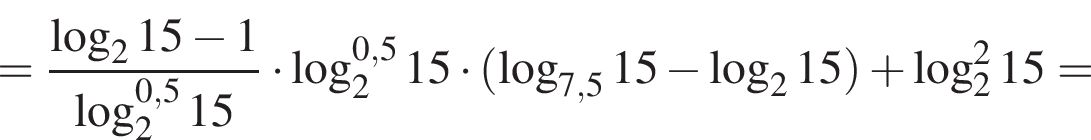
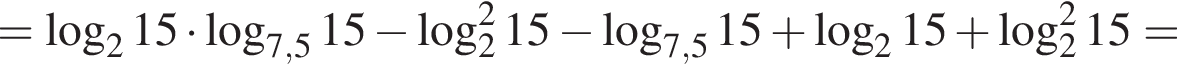
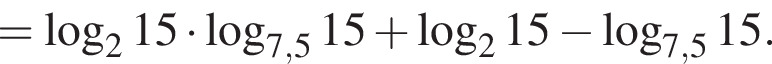
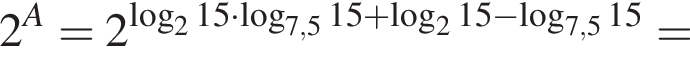
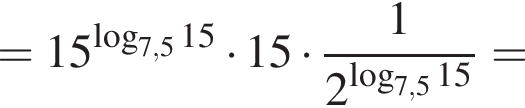
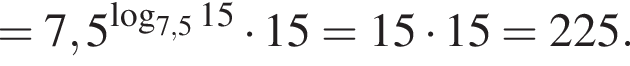
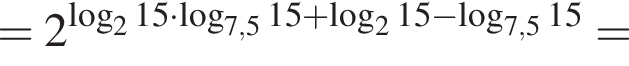
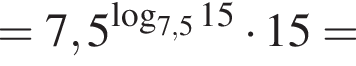
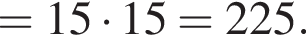
 По теореме о пропорциональных отрезках получаем, что
По теореме о пропорциональных отрезках получаем, что 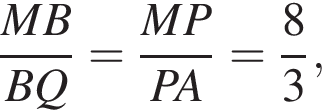
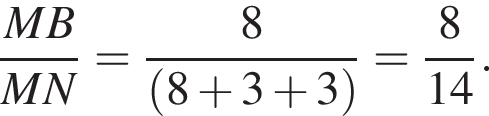
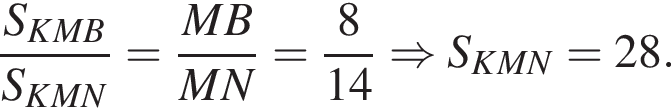
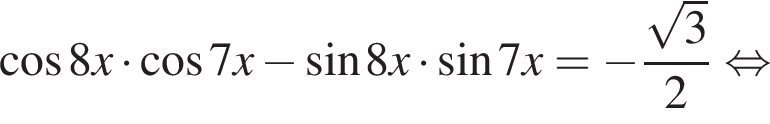
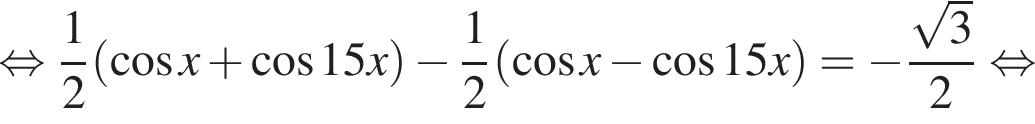
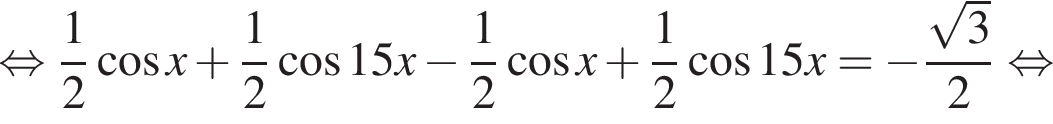
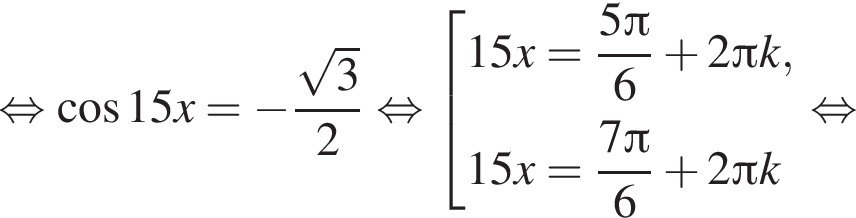
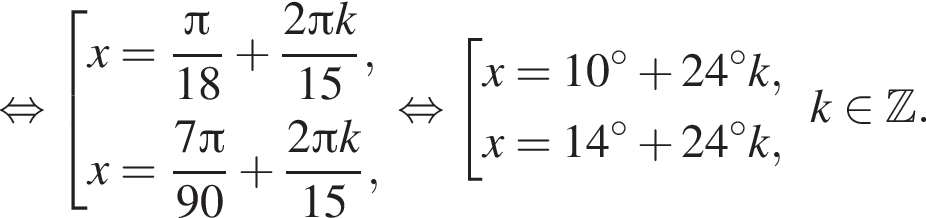
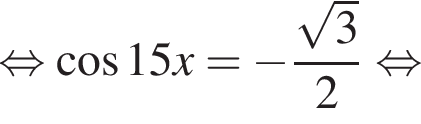
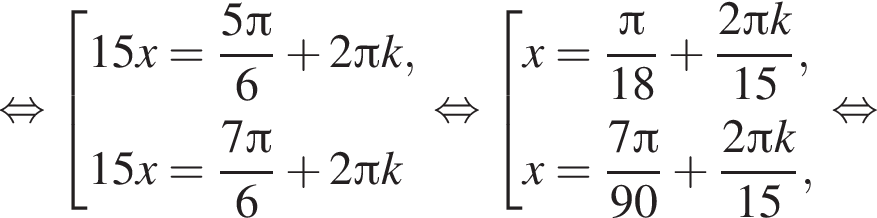
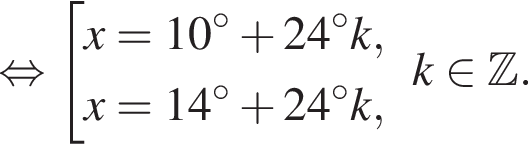
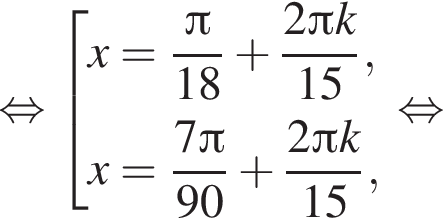
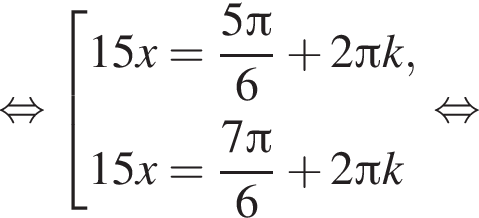
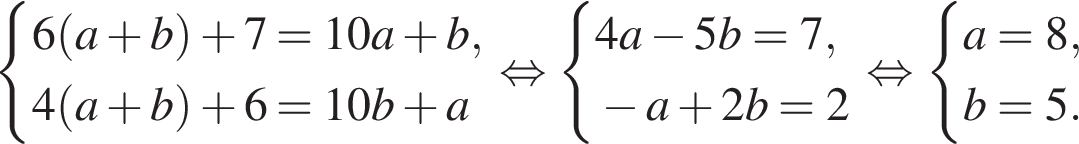
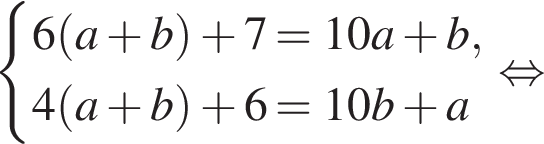
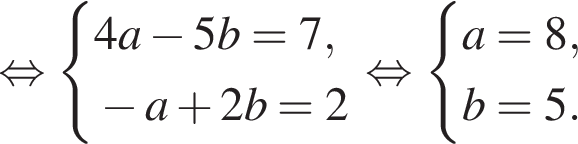
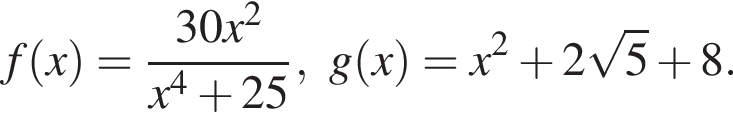
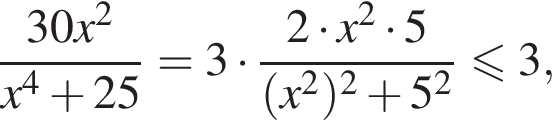 равенство достигается при
равенство достигается при 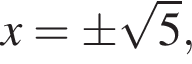 тогда
тогда 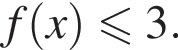
 равенство достигается при
равенство достигается при 
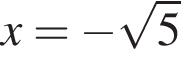 — единственный корень уравнения, тогда:
— единственный корень уравнения, тогда: